写程序累了,来点数学换换口味:) 想起高中时求sin(18°)的一个方法,感觉挺有意思,写下来与大家分享。通过这个方法可以看出它与黄金分割的关系.
我们构造一个顶角A为36°的等腰三角形△ABC,作角∠B的平分线,交AB于D,并作出∠A的平分线,交底边与E,如下图,
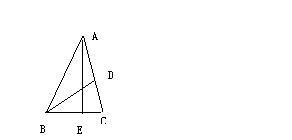
则我们有
△ABC∽△BCD,
从而有,
AB/BC = BC/CD,
即有,
BC^2 = AB*CD
所以,BC =AB* (sqrt(5)-1)/2,
由于AE⊥BC, AE为∠A的平分线,所以,
sin(18°) = sin(∠BAE) = AE/AB = (BC/2)/AB
=(1/2)*(BC/AB)
= (sqrt(5)-1)/4 ≈ 0.618/2 = 0.309
也就是说,sin(18°) 为黄金分割的一半。
作者:豆博草堂